大学1年生で学ぶ数学「解析学・微積分」の要点まとめ,勉強法の解説。 入門用に全体像・概要をわかりやすく紹介
大学一年生で学ぶ数学のうち,「解析学の基礎(微積分)」について
勉強法やポイントを,図表を交えつつ分かりやすく解説。
つまずきがちな微積分の全体像をつかめる。
解析学は,「微小量の厳密な理論」だ。
これを学ぶ理由・価値は何なのか?
また,どのように全体像を把握して学習を進めたらよいのか。
下記は,新入生が「解析学の概要」を理解する助けになるだろう。
(要約) 解析学とは,一言でいうと「微小量の理論」であり,微積分や極限のこと
大学の1年次の数学では,主に「解析学」と「線形代数」の2つを学ぶ。
このうち「解析学」とは,つまり微積分のことだ。
極限や無限を使って,関数の性質を調べ計算する。
解析学のカリキュラムでは,1年生の夏と冬で,
それぞれ以下のようなことを学ぶ。
- 解析学(夏):
- 1変数の,微分と積分。
- ε-δ論法による極限や,関数の収束の扱い方。
- 解析学(冬):
- 2変数および多変数の,微分と積分。
- 複雑な面積や体積の計算により,重積分をつかいこなす。
そして教官にもよるが,1年間の中でたいてい,常微分方程式の解法を教わる。
微分,積分,そして微分方程式。
これが解析学の「1年間の成果」だと言える。
1年次の解析学は,下記のPDFまとめで独学できる。
大学の数学で,微積分(解析学)の講義ノートPDF。演習問題と解答付き(大学1年で学ぶ,1変数と多変数の微分積分学のオンライン教科書) - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140509/UniversityCalculusPDFNoteLinks
- 微分には極限やε-δ論法,級数展開,収束などが含まれる。
- 積分には線・面・体積の積分や広義積分を含む。
- 良質な講義資料を集めた。演習問題と解答もある。おかげで,高い参考書を買わなくて済む。
しかし,無料でぶあつい教科書PDFが手に入るのはありがたいが,
まずは手っ取り早く,全体の概要だけを知りたい。
という人も多いだろう。
そういう人のために,解析学のポイントのつながりを解説するのが本記事だ。
(特徴) 無限小のレベルでの「精密さ・厳密さ」を追求する学問
解析学とは,「無限小のレベルで厳密に正しいかどうか」を突き詰める学問だ。
どれほど細かくしても正しい,という精緻(せいち)で精密な理論を構築する。
たとえば,関数 f(x) と g(x) を比べて,
遠くから眺めると「だいたい一致している」ように見える。
しかし,よく見ると g(x) には,いくつか小さなでっぱりがあって,
細かいところで f と g は互いに一致していないことが分かったとする。

このでっぱりの大きさはεだ。
εをものすごく小さくできる場合,どこまで小さければ,
「f(x) と g(x) は互いに等しい」
と言えるのだろうか?
これは,解析学で学ぶ「関数列の極限・収束」という項目であり,
「微分」を正確に定義するために必要になる考え方だ。
のちのち,解析学の発展分野である「測度論」や「関数解析」にもつながってゆく。
このように,小さくて細かな量を相手にして
精密さを追求するのが解析学だ,と言える。
おもに関数を相手にして,無限にちいさいレベルで厳密か,正確かどうか
を調べることができるようになるのだ。
解析学 - Wikipedia
https://ja.wikipedia.org/wiki/%E8%A7%A3%E6%9E%90%E5%AD%A6
- 解析学(mathematical analysis)とは、極限や収束といった概念を扱う数学の分野である。
- 代数学、幾何学と合わせ数学の三大分野をなす。
- 現代日本においては,解析学の基本的分野は,概ね高校2年から大学2年程度で習う。
独学でも理解できるある程度厳密な解析学の教科... - 高校数学 | Yahoo!知恵袋
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1232378197
一変数の微分積分
→多変数の微分積分(偏微分・重積分)
→ベクトル解析(曲線・曲面上での微分積分)
→微分形式(多様体上での微分積分)
→微分幾何(リーマン多様体上での微分積分)という流れ
- 積分論にはリーマン積分論(区分求積法)とルべーグ積分論(測度論)がある
(価値・意義) 微小量を制する者は,巨大な量をも制する。厳密な理論を展開できるから
では,解析学がどのように役に立つのかを見てみよう。
上の記述において,解析学であつかうのが「小さな量」だと述べた。
ここで,小さいからと言って,
ささいなこと,無視できること…と侮ってはいけない。
「微小な量」を制することで,厳密な理論が展開でき,
その結果として「巨大な量」「現実の物理量」をも制する
ということが可能になるのだ。
これが解析学の価値,そして特徴的なアプローチである。
ここで,微小量から巨大な量(巨視量)へ,というアプローチの
例を見てみよう。
物理法則は,
「ある微小量の変化 = 別の微小量の変化」
という形式で表現される。
これが微分方程式だ。
たとえば,
- 「微小な位置の変化」を dx,
- 「微小な力の変化」を dF
とすると,
バネが生む力は dF = k dx という微分方程式を満たす。
この式の両辺にあるのは,まさに「微小量」であることに注意しよう。

現実世界は「微小量」で記述され,
その微小量を正しく扱うための理論が「解析学」なのだ。
もし微小な量の扱い方を知らないままだと,
微分方程式を正確に記述できず,現実の世界の変化を把握できない。
また,それを積分して解くこともできない。
「微小な量を足し合わせることによって,
ある時点での結論を予測する」のが積分である。
微小な量を,ひとつ残らず,漏れることなく集計しているので
導き出された結論には「集計漏れ」がない。
微小量を相手にしたおかげだ。それが積分という操作。
この積分のためには微分が必要であり,
さらに微分を正しく使うためには,微小量を厳密に間違いなく扱う必要がある。
だから,現実世界を理解するためには,「微小量の厳密な理論」が不可欠なのだ。
それが解析学である。
「物理をどのように学ぶか」
http://lambda.phys.tohoku.ac.jp/~kobayash/com/kyomu_p07/orientation/files/phys_guide.pdf
- 「普遍的かつ定量的な理解」を得るために,物理では数学を使います。
- た何らかの,解釈の余地がない厳密な記述法が必要ですが,数学はま さにそのような目的にかなったもの。
- 物理の計算を行う際には,「微小量」を,イメージを持って使いこなせることが重要です。
- これは,物理法則がしばしば微小な変化に対する系の応答という形で表されることと,また現象の直感的な理解を得る方法として微小量についての展開がよく行われるためです。
ここまでで,解析学の実用的な効用として:
微小量をあつかうおかげで,
- 現象を(微分方程式として)精密に正しく記述でき,
- 集計漏れも防げるので,
- (積分により)正確な予測ができる。
という点が理解できただろうか。
(要点のつながり) 大学1年生の「解析学」のポイントを追いかけるストーリー
さて,解析学の目的や意義,アプローチ方法はよくわかった。
ここからは,具体的な学習項目を紹介し,それを体系的に関連付けてみる。
大学に入りたてのタイミングからはじめて,
1年生が終わるまでの間に,いったい何を身につければよいのか?
1年生の解析学のポイントを,ストーリー形式で考えてみよう。
ただし,1年間の終了した時点,つまりゴールから
逆算して考えてみることにする。
(ステップ1)「多重積分」のためには,1変数での積分や微分が必要。
天下り的にゴールから逆算して考える。
1年生の冬が終わるタイミングでは,「多重積分」が使いこなせて,
複雑な面積や体積を計算できるようになっていればよい。
∫∫∫ dxdydz f(x, y, z) の形をした,多変数の積分である。
これができれば,「リーマン積分」をいちおう使いこなしていることになる。
(ただし,1年次ではまだ「ベクトル解析」の分野までは踏み込まない。)

ところが,ここで注意しておきたいのは
「多変数の計算なんて,人間には計算できないよ!」ということ。
基本的に人間は, 多変数の積分である多重積分をそのまま計算することはできない。
(※コンピュータが数値計算で,数値積分により近似値を求めることはできるけど…。)
そこで,人間が計算できるようにするためには,
多変数の積分は,「1変数の積分」の組み合わせ or 繰り返しに分解される。
∫∫ dxdy f(x, y) = (∫ g(x) dx) ・ (∫ h(y) dy)
のように,xだけの積分と, yだけの積分に分けて考えるのだ。
あるいは,
∫∫ dxdy f(x, y) = ∫ (∫ f(x, y)dx) dy
のように,一変数の積分を繰り返すこともある。
多変数を1変数に分解する,という点では同じことだ。
このような分解・還元・シンプル化をしないと,
人間が計算を進めることはできない。
「人間が計算できるのは, 1変数のみ」なのである。
このシンプル化という発想法は,数学や工学のあらゆる分野に繰り返し現れる。
だから,1年冬学期で「多変数の積分」を可能にするためには,
まずは1年夏学期で「1変数の積分」をマスターする必要があるよね,ということになる。
ここで,「微分積分学の基本定理」によれば,
「積分とは, 微分の逆操作」である。

だから,1変数の積分を実行するためには,
まず1変数の「微分」をマスターしなければならない。
微分積分学の基本定理 - Wikipedia
https://ja.wikipedia.org/wiki/%E5%BE%AE%E5%88%86%E7%A9%8D%E5%88%86%E5%AD%A6%E3%81%AE%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86
- 「微分と積分が互いに逆の操作・演算である」 ということを主張する解析学の定理である。微分積分法の基本定理ともいう。ここで「積分」は、リーマン積分のことを指す。
- 17世紀にこの定理が発見されるまでは、微分法と積分法は,なんの関連性も無い全く別の計算だと考えられていた。
ここまでの学ぶ順番を整理すると,
1変数の微分
→ 1変数の積分
→ 多重積分
ということ。
(ステップ2)1変数の微分のためには,「関数列」や「点列」の極限操作が必要。
多重積分の前準備は,とりあえず1変数の微分に帰着された。
しかし,本当に厳密な意味での「微分」や極限,無限小とは何なのだろうか?
という根本的な問題が生じてくる。
微分とは「瞬間的な(=無限小に短い期間の)変化の割合」を求める操作だ。
しかし,0.01 秒,0.001 秒,…と短くしていった場合,
どこまで短くすれば「無限小の意味で短い」と言えるのだろうか?
また,そのような短い期間での変化の割合をどうやって計算したらよいのか。
こうして,微分の定義の模索・再発見の旅が始まる。
また,関数を微分できる(微分可能)とはどういうことで,
微分できないケースとは何なのだろうか。
たとえば,正弦波 sin(x) の「山」の部分は,なめらかな曲線だから,
もちろん微分できる。
しかし正弦波 sin (ωx) の周波数ωをどんどん上げてゆくと,
関数の波形はものすごくギザギザで,山の部分が無数のトゲみたいになってしまう。

この状態で,この正弦波を微分してよいのだろうか?
どの程度までギザギザした波形は微分してよく,どこからはダメなのだろうか。
ギザギザした波形というのは,現実世界にはたくさんある。
ノイズ・雑音は非常にギザギザしているし,粒子のブラウン運動も同じ。
また,原点でのみ正の値を持つ「δ関数」は量子力学に頻出だ。
こういった関数は,大学からの勉強では非常によく使うので,
「微分できるかどうか,なぜ微分できないのか」という線引きが必要だ。
※詳しくは下記を参照。
ワイエルシュトラス関数 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%AF%E3%82%A4%E3%82%A8%E3%83%AB%E3%82%B7%E3%83%A5%E3%83%88%E3%83%A9%E3%82%B9%E9%96%A2%E6%95%B0
- 連続関数であるにもかかわらず,至るところ微分不可能な関数
至るところ微分不可能殺人事件 - hiroyukikojimaの日記
http://d.hatena.ne.jp/hiroyukikojima/20080101
- 「至るところ微分不可能」というのは:
- 連続(切れ目がない)曲線であるにもかかわらず、ほとんどの部分に滑らかさ(微分可能性)がない
- そこらじゅうがカクカクと曲がってる, とっても不思議な曲線
- 歴史的には、ペアノ曲線とか高木関数とか、幾何ブラウン運動の軌跡などがそれにあたる。
いたるところ微分不可能な関数
http://izumi-math.jp/sanae/MathTopic/takagi/takagi.htm
- 著名な「解析概論」の著者・高木貞治が考えた“高木関数”と呼ばれるグラフ
- 任意の点で, 傾き1と-1の直線が交互に繰り返し交わっている
超関数 - Wikipedia
https://ja.wikipedia.org/wiki/%E8%B6%85%E9%96%A2%E6%95%B0
- 超関数は、連続関数に対する微分の概念を拡張し、偏微分方程式の解空間を拡げた。
- 超関数は, 不連続関数の構成において特に有用であり、物理や工学で扱われる離散的な問題においては、デルタ関数のような超関数を解とするような微分方程式が導かれるため重要である。
このように,微分できるシチュエーションを厳密にはっきりさせないと,
「微分」の議論に矛盾や穴が生まれるので,安心して微分が使えない。
だから,「微分の値がしっかりと定まるのはどんな場合か」という課題が生まれる。
ここで微分とは,定義によれば「関数に対する極限操作」である。
だから,微分に関する理論を整備するためには,
まず「関数に対する極限操作」を得意にならなければならない。
つまり関数の列(関数列)を考えて,その列が無限に続くことを考え,
その列が無限の果てにおいて「収束する」という保証が必要だ。
でなければ,ある関数の微分を
ある定まった(収束した)値として定義できなくなってしまうから。

さて,そのように関数の列を考えるためには,まず先に何を考えるべきか?
関数 f(x) の列は,x 軸上の各々の1点だけに注目すると,
ある一つの値 x に関する「点列」である。
点列の集まり,あるいは点列を拡張した概念が「関数列」なのだ。

だから,関数列 { f(x) } の極限操作を考えるためには,
まず先に,一つの値 x に関する点列の極限操作に習熟する必要がある。
そういうわけで,まずは「点列の極限操作」が目下の課題となる。
ここまで学ぶことを整理すると,
点列の極限操作
→ 関数列の極限操作
→ 関数列の収束
→ 微分が存在し,微分可能であること
→ 1変数の微分の完成
となる。
(ステップ3)「点列の極限」と「関数列の極限」には,収束法や連続性に応じた橋渡しが必要。
もちろん,上記の流れには例外もある。
「点列」を拡張して「関数列」にするわけだが,
時として,その両者の極限にはギャップもあるためだ。
点列の計算結果を拡張しても,
関数列の計算結果とは性質が異なってしまうケースがあるのだ。
これが関数列の収束のバリエーション,
つまり「各点収束」と「一様収束」の違いである。
そして,このような関数列の収束の違いは,
関数が「連続」かどうかにも深いかかわりがある。
「連続性を保ちながら収束」するのが一様連続であり,
「連続性が失われるかもしれない収束」が各点収束なのだ。
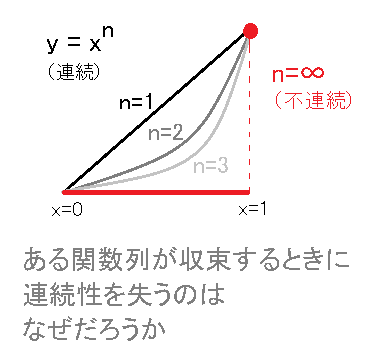
当然ながら,「微分したら不連続になってしまった!」
などという事態は避けたいので,一様収束を前提としたほうが
微分の議論がスムーズに進むことになる。
※参考:点列の極限は,関数列の極限とは異なる:
関数列と関数項級数
http://www.math.keio.ac.jp/~iguchi/Lectures/pdf/2011/Note_MA_6.pdf
- 実数列やユークリッド空間における点列の収束という概念は,ただ一つしかなかった
- それに対し,関数列になると, 無限に異なる収束の概念が存在する.
一様連続と一様収束 ~ 木を見て森も見る - Imaginary & Imaginative.
http://taketo1024.hateblo.jp/entry/uniform
- 「関数列の極限」は「数列の極限」とは違って…
- 極限関数で急に段差ができたり,トゲが出てきたり、
- あるはずのものがなくなったり性質が変わったり。と色々な豹変をしてしまう
- そこで関数列に何らかの制約を加えて、こういうギョッとすることが起きないようにしたい。
- そこで出てくるのが「一様収束」。
- 関数を全て集めた「空間」を考えると、「関数列の一様収束」とは「関数空間における点列の収束」
関数列が一様収束すれば,さまざまな良い性質を満たせるので価値がある。
なので,関数列の収束方法を調べると役立つ:
各点収束と一様収束の違いと具体例 | 高校数学の美しい物語
http://mathtrain.jp/ichiyosyusoku
- 「関数として近づく」というのを数学的に定義
- 「各点収束」と「一様収束」という二つの概念があり,一様収束の方が強い。
- 一様収束が嬉しいのは,「連続関数列の一様収束極限はおなじく連続関数」という定理が成立するから。
「各点収束と一様収束」
http://www.misojiro.t.u-tokyo.ac.jp/~murota/lect-kisosuri/uniformconv070914.pdf
- 一様収束は,何のための概念なのか。その目的について。
- 連続関数の 各点収束 極限は,連続関数とは限らない
- 連続関数の 一様収束 極限は,連続関数である(連続性を保ちながら収束できる)
一様収束(いちようしゅうそく)とは - コトバンク
https://kotobank.jp/word/%E4%B8%80%E6%A7%98%E5%8F%8E%E6%9D%9F-31414
- 一様収束が重要な理由は、次の定理が成立するためである。
- (1)連続関数の一様収束極限は、また連続関数である。
- (2)関数列が一様収束すれば、極限関数の積分は、各関数の積分の極限に等しい。(=項別積分ができる)
下記の点をしっかり押さえよう。
- 関数の連続性の違い
- 関数列の収束方法の違い
収束法によって,極限の計算結果が連続かどうかも変わってくる。
そして,もし収束後に連続性を失うのであれば,それ以上は微分もできなくなる,というわけだ。
収束法をはっきりと区別できるようになれば,
- 「点列の収束」と「関数列の収束」をきちんと橋渡しでき,
- 「点列の極限」から「関数列の極限」へ,矛盾なく話がつながる。
そして関数列の極限操作である「微分」へ,と
矛盾なく移行できることになる。
ここまでを整理すると,学ぶ順番として
点列の収束
→点列の極限操作の完成
→関数の連続性
→関数列の収束方法
→関数の極限操作の完成
→関数の微分
といった具合になる。
なので,話を元に戻して,
結局「点列の収束」が目下の課題となる。
(ステップ4)点列の収束のために「ε-δ論法」が必要。(※最大のヤマ場)
そして・・・ここが,大学に入りたての数学のヤマ場だ。
大学1年生の苦手分野ナンバーワン,
大学からの授業内容についていけなくなる理由の筆頭ともいわれる,
あの悪名高き「イプシロン・デルタ論法」が出てくるからだ。

点列が無限に続くとして,
その列があとのほうで「意味のある値におさまる」ことを保証するのが
ε-δ論法である。
正確に言うと,関数の極限がε-δ論法なのに対し,
そのベースとなる点列の極限を ε-N 論法と呼ぶ。
これを学べば,極限値とは何なのか,
変動して揺れ動く変数が,誤差をどんどん減らしてゆき
しまいには一定値に収束する…とはどういうことか。
キッチリと定義することが可能になる。
大学数学のε-δ論法は,関数の極限の定義を厳密化。わかりやすい意味は,yの誤差を小さくするようなxの誤差が存在ということ
http://study-guide.hatenablog.jp/entry/20150405/p1
- わかりやすくイプシロン・デルタを言い換えると 「yの誤差」をいくらでも小さくできるような「xの誤差」が必ず存在する, という意味だ。
- ここで,「yの誤差」とはεのこと。 「xの誤差」とはδのことだ。
イプシロン・デルタ論法を理解する際には,
単なる論理記号の並びと見てはダメだ。
「無限に細かく観察した時に,
観察のレベルが細かければ細かいほど,
いっそう限りなく誤差が小さくなり,近づいてゆく…」
という,極限のイメージを想像することが大事だ。
それがまさに「無限」の定義でもある。
点が収束すれば,「点の集まりである関数」の収束もわかってくる。
そういうわけで,関数を自由自在に操るためには,
まずは一つの点,点列の動きを完璧につかむことからはじめよう。
(ステップ5)「極限の収束」を定義できれば,実数上に存在するさまざまな数や区間を正しく定義できる。
こうして,「点列の収束」を厳密に定義できれば,
それはつまり「極限の収束」「極限値」を定義したことになる。
これにより,解析学の根本的な目的である
「無限小の意味で正確」というスローガンの第一歩を達成できる。
そうすると,実数の数直線上に存在するありとあらゆる数を,
はっきりと区別して,厳密に定義することもできるようになる。
たとえば,0.999999... のように「9」が無限に続く数は,
厳密にいって「1」に等しい。
なぜそう言えるのだろうか?

解析学は「無限小」を正しく扱う学問なので,
0.9999... と「1」の間に存在する微小な誤差 0.000000...01
の大きさを,正しく評価できるためだ。
ある数と別の数が「互いに厳密に等しい」ことを主張できる。
また別の例として, π という無理数を例に挙げれば,
これは3という整数ではないし,3.14159265という有限桁の小数でもない。
どれほどπの桁を増やしても,無限にπを精密化でき,
いかなる他の有限桁の小数とも区別ができる。
無限小の意味で正しさ・精度を追求できるわけだ。
ここに解析学の考え方がある。
こうして,「有理数と無理数」が厳密に区別され,
数直線上での「区間」という集合も正確に定義できることになる。
これこそ実数論,そして集合論・位相論の幕開けである。
「集合と位相」の講義ノートPDF。位相空間論に入門するためのオンライン教科書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140628/SetAndTopologyPDFLectureNotes
- 数とは,集合である。 そして集合の各要素に対し「近さ」(距離) の概念を導入すれば,位相空間になる。
- 何かの集合や空間を定量的に扱うには,位相の考え方が必要になるという事だ。
大学の「数論」(初等整数論と,代数的数論)の講義ノートPDF。独学用のオンライン参考書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140704/NumberTheoryPDFLectureNotes
- (1)整数を扱う初等整数論
- いわゆる「整数問題」というやつの体系と思ってよい。
- (2)群・環・体を使った代数的数論(Algebraic number Theory)
- もっと本格的で,「代数的な数」を扱い,自然な流れでガロア理論が出てくる。
集合や位相を論じるためには,
極限操作を使った「ε近傍」という概念が基本になる。
その概念をもとにして,各種の「被覆」となる新しい集合を考案でき,
関数解析やルベーグ積分などの測度論へ発展してゆけるというわけだ。
「ルベーグ積分」の講義ノートPDF。測度論と確率論の入門(演習問題と解答付き) - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140510/LebesgueIntegralMeasurePDFNoteLinks
- 量を定義しにくい複雑な集合を扱う場合, その集合の大きさを積分や確率で「測る」ために,測度が必要。
- 測度論の入門としてルベーグ積分を学ぶと, 関数解析や確率論,数理ファイナンスなど解析学の応用分野で, 複雑な集合の扱いに困らなくなる。
「無限小」を正しくあつかえるようになることで,
さまざまなメリットが生まれる様子がわかるだろうか。
単に微分や積分の計算ができるだけでなく,
「実数」や「区間集合」などの超基本概念をも,精密に定義することができる。
無限小をあつかう解析学には,価値や応用がたくさんある…
という点に, 自信を持ってほしい。
(実用性) 無限小がわかると,精度のよい「近似」が可能になる(テイラー展開)
さて,解析学では,「とても小さい量」を厳密に扱えるようになるのであった。
「微小量 / 微小量」という比・分数のようなものを考えれば,
それは微分の値になる。
これによって正確な微積分が可能になるので,
「微分方程式を解いたりできる」という価値が生まれていた。
では,微小量を分数とか比にしないで,
「微小量」という単一の値を考えたらどうなるか?
これを考えることによって,解析学のもう一つの価値が明らかになる。
それは,誤差の少ない近似計算だ。
解析学は「微小量の理論」なので,微小な誤差をコントロールでき,
できるだけ正確な近似値を求めたい,というニーズにこたえてくれる。
たとえば sin(0.5) の正確な数値や,e の値などを精密に計算する場合,
コンピュータに計算方法を教えたうえで,有限桁で計算を止める。
つまり,コンピュータに近似計算をさせて,誤差を一定範囲内に抑えるわけだ。
このような近似計算に役立つのが,テイラー展開・マクローリン展開であり,
その近似計算の誤差がどれぐらい小さくできたのか?という
誤差の精度を評価するために使うのが,ラグランジュの剰余項だ。

テイラー展開とは,関数を多項式で表現すること。
その剰余項とは,テイラー展開において,有限の多項式で近似した際の誤差である。
テイラーの定理 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%86%E3%82%A4%E3%83%A9%E3%83%BC%E3%81%AE%E5%AE%9A%E7%90%86#.E5.AE.9A.E7.90.86.E3.81.AE.E4.B8.BB.E5.BC.B5
- テイラー多項式は「漸近的に最もフィットする」唯一の多項式である。
- テイラー展開の剰余項は,テイラー多項式で近似するときの近似誤差である。
補足資料:Taylor展開について
http://gandalf.math.kyushu-u.ac.jp/lectures/bibun_sekibun/notes/appendix1.pdf
- sin 0.1 の近似値を求めたい.
- 今 Taylor 展開の第 1 項のみを取ったとき,誤差はどの程 度の値になると考えられるか.
マクローリン展開、テイラー展開の誤差について - 公式でマクローリン展開... - Yahoo!知恵袋
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1118011796
- 剰余項は誤差そのもの
テイラー展開を使うと,ものごとを「大きいものと小さいものに分解」できる。
f(x) = (大きいもの) + (中ぐらいのもの) + (微小で無視できる量) + ....
そして,分解した結果,「小さいものは省いてしまえ。」
「最初の1つか2つの大きな項だけで,じゅうぶん近い数値になるよね。…」
というのが,テイラー展開による近似計算である。
その結果が, sin x ≒ x とか, cos x ≒ 1 - x^2 /2
のような,1つか2つの項を使った近似値。というわけだ。
この場合は3乗から先の項を,テイラー展開の誤差・剰余項として無視している。
こうしてコンピュータは sin とか cos の値を計算できるようになる。
コンピューターは,さまざまな数値の近似値を求めるために,
内部でしょっちゅうテイラー展開しているのだ。
もし,近似の精度を上げたいのであれば,項の数を増やせばよい。
その気になれば,無限に項を増やすことができる。
テイラー展開は「無限級数による関数の表現」なので,
後ろのほうの項は微小量となり,
項を増やせば増やすほど,いくらでも精度があがってゆく。
このようなテイラー展開の性質を使えば,ネイピア数 e の値を計算して
e が無理数であることを証明することもできる。
つまり,e の値は,テイラー展開の後ろのほうに来る微小量を使って
いくらでも無限に桁の精度を上げられるので,
どのような循環小数とも異なっており,有理数ではない・・・。
という結論を導くことができるのだ。
※詳しい証明は下記を参照。
ネイピア数の無理性の証明 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%8D%E3%82%A4%E3%83%94%E3%82%A2%E6%95%B0%E3%81%AE%E7%84%A1%E7%90%86%E6%80%A7%E3%81%AE%E8%A8%BC%E6%98%8E
- 証明は背理法による。すなわち、e が有理数であると仮定して矛盾を導く。
- eを級数表示して,その級数の後ろの微小な部分が無限に続くという根拠によって,無理性を示せる。
微分積分学入門 - text_calculus.pdf
http://www7b.biglobe.ne.jp/~h-kuroda/pdf/text_calculus.pdf
- 例題 6.6. ネピア数 e は無理数であることを示せ
- テイラー展開し,ラグランジュの剰余項を使った証明。
このように,近似計算以外にも,理論的な側面で
テイラー展開や級数和が役に立つ,ということがわかる。
テイラー展開による近似計算は,工学系の数値計算では非常によく使う。
また,物理学でも1次近似,2次近似,…として頻繁に現れる。
1年生で学ぶ解析学の中で,のちのちもっとも頻繁に使用することになるだろう。
近似値の計算や誤差の評価を,侮ってはいけない。
こういう実用的な数値計算のおかげで,人間の命が助かるのだから。
たとえばもし,円周率πの正確な近似値がほぼあいまいにしか分からなかったら,
ロケットが地球のまわりを飛ぶ際の円周の長さも正確には分からなくなるわけで,
円周軌道の途中で,ロケットは燃料切れになってしまうだろう。
たかが微小量も,数百万倍,数十億倍すれば,無視できない量になる。
そうやって誤差が膨らんだせいで事故が起きる。
そのような事態を避けるために,正確に円周を計算する必要がある。
計算の誤差も,範囲を指定して,±1% のように誤差評価しておけば
誤差を考慮に入れて余裕・ゆとりをもった必要十分なプランを立てることができる。
近似値と誤差は互いに切り離せない関係にあり,
誤差評価のおかげで,ゆとりをもった現実的な計画が可能になるということ。
微小な量を制すれば,テイラー展開による近似値を役に立てることができる
というのがよくわかっただろう。
以上が,「微小量」をテーマとした,1年生の解析学の概観だ。
(1年生の終盤) 多変数の解析学は,「ベクトル解析」の一歩手前まで
ここまで,解析学とは「微小な量の学問」だ,と述べてきた。
たしかに,序盤からしばらくのうちはその通りだ。
大学1年生のうちは,理論の土台となる厳密さに気を配る必要がある。
だが,いつまでも細かいことにばかり気を取られているわけにはいかない。
土台となる基礎理論を習得したら,それを活用して
先に進んでゆき,考察の対象を広げてゆかなければならない。
「無限小の細かい誤差」だけを主要な注目対象とするのではなく,
視界を広げて,多変数関数がおりなす曲線や曲面を分析する。
微分幾何学のはじまりだ。
とはいえ,大学1年生のうちは,解析学であつかえる対象もごく限られている。
たとえば,下記のような問題設定だ。
3次元空間内に,2変数関数 z = f( x, y ) がある。
この関数が作る曲面は,どこに極値・停留点があるか?

この問題を解くためには,多変数関数を「xだけで微分」
または「yだけで微分」する必要がある。
これが偏微分である。
そして,x方向とy方向のそれぞれについて,
増減や停留点などの特徴的なポイントを見つけ出し,
x方向とy方向で情報を合成して,曲面の形を推定することになる。
ここで,x方向とy方向の情報を合成して結論を出すためには
ヘッセ行列(ヘッシアン)が必要だ。
これは大した計算ではないが,いちおう行列式なので,
線形代数と関係があるということになる。
- 多変数関数の微分では,ヘッセ行列からヘッシアンを作って極値判定,
- 多変数関数の積分では,似たような概念として,ヤコビ行列からヤコビアンを作って変数変換。
という具合に,行列を使い分ける。
偏微分の階数が1階なのか2階なのかの違いなので,難しい概念ではない。
※参考:
鞍点
http://mathweb.sc.niigata-u.ac.jp/topic/saddlept.html
- ちょうど尾根と谷にはさまれている場所を形成している場所を,鞍点(あんてん)と呼ぶ。
- 微分すると零なのに、鞍点は谷底ではないので極小でなく,また丘の上でもないので極大でもない。
- 「極値をとらない停留点」とも呼ばれる。
(1)鞍点と停留点の違いは?(2)鞍点か停留... - 数学 | Yahoo!知恵袋
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11118320451
- 停留点とは, x での偏微分 f_x と, y での偏微分 f_y がともに 0 となる点。
- 停留点には極値もあれば、極値でない場合もある。
- 極値でない場合のひとつが鞍点であるが、他にもたくさんある。
- 例えば、z(x, y) = x^3 の原点 (0,0) は停留点だけど、極値でも鞍点でもない。
微分演算子:勾配ベクトル、ヤコビ行列・ヤコビアン、ヘッセ行列・ヘッシアン、ラプラシアン
http://www.ne.jp/asahi/search-center/internationalrelation/mathWeb/Differentiation/PartialDifferential2VarFnctn/GradHessian.htm
- 「2変数関数f ( x, y )のヘッセ行列」とは、2変数関数f ( x, y )のすべての第二次偏導関数を並べた2×2行列のこと。
ヤコビ行列 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%A4%E3%82%B3%E3%83%93%E8%A1%8C%E5%88%97
- 多変数ベクトル値関数 f のヤコビ行列は、f の各成分の, 各軸方向への方向微分を並べてできる行列
しかし,大学1年生では,これが限界である。
なぜなら,本格的に曲線や曲面を解析したい場合,
どうしても「ベクトル解析」を先に学ぶ必要があるからだ。
grad, div, rotを駆使したベクトル解析学は,
一般的に言って,1年生でマスターする範囲ではない。
(ベクトル解析よりも先にフーリエ解析を習得したほうがよい。)
なので,1年生のうちに「多変数の解析学」で学べるのは
微分幾何学の中でも,曲線・曲面論のほんの入門部分にすぎない…と言える。
物理数学で,「ベクトル解析」の教科書PDF(演習問題と解答つき) 入門用の講義ノート - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140612/VectorAnalysisPDFLectureNotes
- 大学の物理では,ベクトル場を数学的に表現する。
- 電磁気学や流体力学では,基本的な定理を言い表すだけでも,ベクトル解析を避けて通れない。
- ベクトル解析は,物理を表現するための「言語」だと思ったほうがよい。
大学の物理で,振動・波動論とフーリエ解析学の講義ノートPDF。 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140619/WaveAnalysisPDFLectureNotes
- 「振動波動とフーリエ解析」は様々な分野の土台になっているので,非常に重要という事になる。
大学の数学で,「微分幾何学」の基礎の講義ノートPDF。曲線・曲面の幾何で,多様体論に橋渡しする - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140629/CurvesAndSurfacesDifferentialGeometryPDFNotes
- 幾何(微分幾何)の初歩として,まずユークリッド幾何からはじめ, 後になって多様体・微分形式・リーマン幾何を学べるよう準備する。
- この入門段階の学習目安としては, 「ガウス・ボンネの定理」(積分=位相不変量 の形)を使い, 「微分幾何」と「位相幾何」を結ぶことが目標として挙げられる。
先を焦る必要はない。
電磁気学の中級レベル以降から,ベクトル解析の必要性が生まれ,
そこでみっちり計算演習することになるので…。
逆にそれまでの間は,ベクトル解析の必要性を理解できないだろう。
電磁気学の講義ノートPDF (演習問題と解答つき) 大学の理論物理の教科書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140615/ElectroMagnetismPDFLectureNotes
- (1)教養科目としての初歩的な電磁気
- (2)理工系の専門科目としての本格的な電磁気(=物理数学をバリバリ使う)
電磁気学講義ノート:マクスウェル方程式のためのベクトル解析 (1)内積・外積の計算を簡素化 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20091115/p1
- ベクトル解析と言えば内積と外積。まずは,これらを簡単に計算したい。
- 内積を簡単に書くために,アインシュタイン記法
- 外積を簡単に書くために,イプシロン(レビ・チビタのテンソル)とクロネッカーのデルタ
また,多変数の解析学において,
1年生の間に学ぶ項目の一つとして「全微分」がある。
熱力学では,全微分と編微分の計算づくしだ。
しかし,ここでも「全微分の本当の意味」は,まだ理解できないだろう。
なぜなら,1年生の間,全微分を直接そのまま相手にすることは少ないからだ。
2変数に関する全微分を考えはするものの,
実際の積分計算の際には,片方の変数を固定する。
そして,単なる1変数の微分に置き換え,1変数で積分して計算結果を出す。
たとえば,気体の体積 V を,温度 T と圧力 p を使って
という全微分で表したとしよう。
これは,Vが変化するときの全ての原因を,1次近似で足し合わせるという意味。
そして,先に述べたように「人間は多変数の式を積分できない」ので,
この式に対する積分計算を実行するためには,変数を1つだけにしぼる必要がある。
そのため,たとえば「圧力は一定」という制約を付け,
dp = 0 のもとで「定圧変化」を計算することにする。
これなら人間でも積分を計算できる。なにしろ1変数だからね…。
こうして積分の結果として V の変化が分かれば,仕事 W の量もわかり,
気体の内部エネルギー U の変化が分かる・・・という算段だ。
ここで,計算の際には必ず,何か1つの変数を「一定」とおくことに注目しよう。
せっかく2変数で全微分形を書いたのに,
計算するときには1変数に限定されるわけだ。
こういう用途でしか全微分を役立てるチャンスがないので,
全微分で「多変数をいっぺんに扱っている!」という実感がまだわきにくいはず。
1年生の間はそれでよい。
全微分とは偏微分の線形和で,「変化の原因」を全て足し合わせること - 勉強メモ (大学の講義動画や,資格試験の対策)
http://study-guide.hatenablog.jp/entry/20140513/p1
- 部分的な性質を調べる時には偏微分を使う。
- 全体的なトータルの変化を計算する時には,全微分を使う。
- そして,「部分的な変化の合計」が「全体の変化」になるので, 全微分を求めるためには偏微分を足し合わせることになる。 というわけだ。
熱力学・統計力学・統計物理学の講義ノート (PDFやオンライン教科書。化学熱力学を含む) - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140504/ThermoDynamicsStaticalPhysicsPDFNoteLinks
- 物質の「ミクロな性質」と「マクロな性質」の掛け橋を作ることが目的。
以上で,1年生の解析学で学ぶ「多変数」分野の概観も終えたことになる。
(まとめ)要点の復習
ここまで概観してきた内容をまとめてみよう。
微小量の理論:
- 点列の極限と収束
- ε-N論法
- 関数列の極限と収束
- ε-δ論法
- 収束法の違い,連続性
- 微分可能と微分
- 近似と誤差
- テイラー展開と級数
- 剰余項
- 積分
- 微分積分学の基本定理
- 一変数の微積分の計算演習,数をこなす
多変数の分析:
- 曲線と曲面
- 極値の分析
- 偏微分
- 全微分
- 偏微分の線形和
- 熱力学への導入
- 重積分
- 面積や体積の計算演習,数をこなす
別途:
- 微分方程式,数をこなす
- フーリエ解析(1年生の終盤までに)
こういった「流れ・全体像」を把握したうえで,
実用的な演習問題をこなしてゆくことが重要だ。
とくに,解析学の着眼点・発想法である
「微小量がなぜ重要なのか?」という点を意識していれば,
ある概念が何の役に立つのか分からず道に迷う…ということもない。
その点は,本記事で繰り返し力説した。
もっとも,解析学だけでなく,
代数や統計による発想法も同じぐらい重要だ。
なので1年生の間は,解析の基礎と微分方程式論に加え,
線形代数と統計学の初歩をみっちり身に付けよう。
これら全てが,2年生以降に進むための基礎となる。
線形代数(行列論と抽象線形代数学)の講義ノートPDF。演習問題と解答付き - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140505/LinearAlgebraMatrixPDFNoteLinks
- 行列論の入門から始め, 逆行列, 固有値, 対角化・2次形式 などを扱い,線形空間の議論に進んでゆく。
- そして線形空間の議論では「抽象線型代数」が扱われ, 正規直交基底, 内積・ノルム などを学ぶ。
微分方程式の講義ノートPDF。例題と解答付き (常微分方程式の初歩的な解き方を勉強) - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140606/OrdinaryDifferentialEquationPDFLectureNotes
- 微分方程式は,大学1年で必ず押さえておこう。
- そうしないとあちこちで(ほとんど全分野で!)つまづいてしまう。
- 物理や工学の他にも,化学反応,生き物の個体数,価格の変動…などなど, 「数式で動きをモデリング」する時に何にでも使う。早いうちにマスターしよう。
- とくに解が厳密に求められるケースでは, 解き方のパターンを一通り押さえておく必要がある。
大学で学ぶ「統計学」の,入門用の講義ノートPDF。データ分析や確率統計の基礎 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140611/StatisticsPDFLectureNotes
- データがあふれる時代なので,データの扱い方を身につけよう。 たくさんのデータを扱うときには,自然と統計学が必要になる。 データの特徴を見抜いたり,部分的な情報から全体を推測したり,仮説を立てて検証したり。
(その先へ) 大学2年生からの発展
1年生の解析学を終えると,その先には何が待っているのだろうか?
解析学の発展分野を知っておこう。
まず,1年生の間は,実数の範囲だけで関数を議論していたことを思い出そう。
その議論の土台を,複素数の範囲に拡張し,
複素平面上での関数の性質を考えるのが複素函数論である。
こうすることで,積分の計算の幅が広がり,関数の性質もよりよくわかる。
少なくとも3年生になるころまでには,
複素解析もしくは函数論を学び終えているはずだ。
複素解析・複素関数論の講義ノートPDF。演習問題と解答つきのオンライン教科書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140603/ComplexAnalysisPDFLectureNotes
- 複素函数論を学ぶ際のスタンスは, 複素解析を「使う側」(工学)と, 複素解析を「証明する側」(純粋な数学) の2手に分かれる。
- それぞれ「関数」と「函数」のように書き分けることが多い。
1年生のうちに,力学の講義で,
常微分方程式を目にする機会がそれなりにあっただろう。
また1年冬学期から先は,電磁気や振動・波動論,量子力学などに触れて
偏微分方程式を解く必要に迫られることも多い。
偏微分方程式は,2年生の間には体系的に知っておくとよい。
そうすれば,専門課程での実用的な解析計算の準備が整うから。
偏微分方程式の講義ノートPDF。解き方や分類の基礎を学ぶ入門用の参考書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140608/PartialDifferentialEquationsPDFLectureNotes
- 物理や工学では偏微分方程式のオンパレードである。
- ここにアレルギーがあると,理工系の勉強が必ずどこかでつっかえる。 マスターしなくてもいいから,パターンやセオリーを知っておこう。
また,解析学の計算をプログラミングしてコンピュータに行わせるためには,
数値計算法の一種として,数値解析に通じておく必要がある。
これも,教養課程から専攻のカリキュラムへと切り替わるころには学ぶ必要がある。
もっとも,数値解析では
1年次の解析学,微分方程式論などを前提として話が進むので,
基礎固めを優先したほうがよいだろう。
また,1年生の間に解析学で学んだ中に,
関数の収束や連続性に関する細かな議論があった。
あなたは,その部分を「おもしろい」と思ったか?
大多数の人はそう思えないのだが,
もし「おもしろい」と感じたのであれば,
あなたには「関数解析」の世界が向いているだろう。
これらは,量子力学や信号処理論の基礎理論を整備するのに役立つ。
工学系だと必須ではないが,理学系・理論系に進むためには
3年次までに押さえておこう。
「関数解析学」の講義ノートPDF (Functional Analysis) 入門用の教科書 - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140616/FunctionalAnalysisPDFLectureNote
- 関数解析では,「物理で使う数学」に対して,厳密に数学的な裏づけを与えることができる。
- また,「偏微分方程式の解となる関数の性質を,あたかも線形代数のように考える」ためにも必要。
- 関数解析は,応用数学の理論的な裏づけだと思えばよい。
なお,数学科の学生であれば,
早いうちにリーマンゼータ関数を攻略しておこう。
これは解析的数論の要であり,現代数学のマスコットのようなものだ。
物理学でも理論系で突き詰めると,じきに出会うことになる。
学習のタイミングとしては,複素函数論を習得した後で2年次のうちには…
と言いたいところだが,意欲的な学生諸氏は,
数学を志した時点で1年次のうちに,すでに独学で学び終えているはずだ。
現代数学の最重要な関数,「リーマン・ゼータ関数」の教科書PDF。素数定理・リーマン予想を勉強するノート - 主に言語とシステム開発に関して
http://language-and-engineering.hatenablog.jp/entry/20140529/ZetaFunctionPDFLectureNotes
- ゼータ関数は,現代数学において最も重要な関数であり,解析的整数論の要だ。
- またゼータの特殊値を具体的に計算すると,物理学への実用的な応用が多いことにも驚かされる。
解析学が「微小量をあつかう学問」であり,
「厳密に正しい理論を構築するための基礎」であるという点をここまで見てきた。
大学1年生の間,またその後にも,
数学書を読み進める際に,この解説記事を何回も読み返してみよう。
点と点がつながって,知識全体が整理されるはずだ。
本記事で掲載した解説が,大学1年次とそれ以降の生活で時間を浪費せず
有意義に過ごして将来へつなげるための助けとなれば幸いだ。



