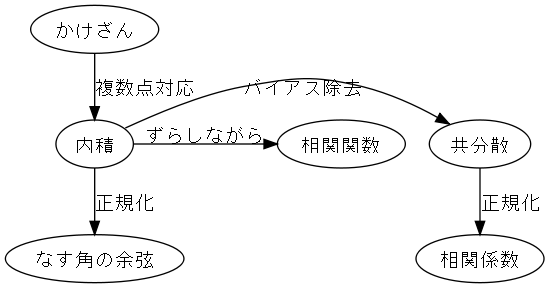
「相関係数とは何か？」 を体系的に理解するための６ステップ

実は，下の６つは，同じものである。

• かけ算
• 内積
• なす角の余弦
• 共分散
• 相関係数
• 相関関数

これらは６つとも類似度を算出するためのツールだ。

（↑まとめ画像）

これらを１つずつ解説・検証する。

（１）かけ算：　符号を見れば，数と数（スカラーとスカラー）の類似度がわかる。

アルゴリズム：

・２つの数 a と b を掛け合わせて，符号を取る。
これを数式では sgn( ab ) と書く。

・結果が正なら，２つの数は類似しており，互いに同傾向である。
	
・結果が負なら，２つの数は類似しておらず，互いに反対の性質を持つ。
	
・結果が0なら，a, b は比較対象のセットとして不適格である。

ここで言う類似度は，数直線上での向きとして定義できる。

aが正の数なら，aは数直線上で右向き。

負の数なら，左向き。

0は向きを持たない。

例：a = 3, b = -2 の図


　−　　　-3　　 原点 　+3　　　　＋
　――――――――Ｏ―――――――→

　　　　　　b ←―・――→ a

　 ab ←―――――・


積 ab の符号が負なので，a と b は類似していない。
(実際，数直線上では逆向き)

当たり前と思うだろう。

だが，この「積を取って正なら同傾向」という概念は，後で姿形を変えて随所で出てくる。

（２）ベクトルの内積：　（１）を複数回行なうことにより，信号と信号（ベクトルとベクトル）の類似度がわかる。やはり符号を見る。

前項のかけ算の「実行ペアの数」を複数にしたものが内積。

なお，「数が複数並んでいるもの」のことを一般には信号と呼んだり，ベクトルと呼んだりする。

数値が複数並んでいるという事はその並びは「波形」を作るから，信号と呼べるのだ。「配列」でもよい。

アルゴリズム：

・２つの信号（ベクトル）

	A = ( a_1, a_2, ..., a_n )
	B = ( b_1, b_2, ..., b_n )

　について，その内積は
	
	A・B = a_1 b_1 +  a_2 b_2 + ... + a_n b_n

　である。
　つまり，成分ごとにかけ算をして足し合わせるだけ。


・内積が正なら，２つの信号は（上がり・下がりのタイミングが）同傾向。

・内積が負なら，２つの信号は逆傾向。

・内積が0なら，２つの信号は種類が異なり，
　傾向に類似点と呼べるものはない。
　（これを直交と言う。）

具体例として三角関数を考えるとわかりやすい。

	A = ( 0, 1, 0, -1 )　　… sin( x ) のような信号
	
	B = ( 0, 2, 0, -2 )　　… 2 sin( x )
	
	C = ( 0, -1, 0, 1 )　　… - sin( x )
	
	D = ( 1, 0, -1, 0 )　　… cos( x )


	ベクトルの意味で内積を取ると，それぞれの信号の類似度は

	
	　A・B = 4 で正だから，傾向が類似している。
	　事実，Aの波形を縦に拡大するとBになる。

	　A・C = -2 で負だから，逆傾向である。
	　事実，Aの波形を縦方向に裏返すとCになる。

	　A・D = 0 だから，直交している。
	　Aの波形を拡大しても，裏返しても，Dにはならない。
	　つまりAとDでは信号の種類が全く異なる。


	となる。

（３）ベクトルがなす角の余弦：　（２）の類似度の数値を， -1（完全に異なる） 〜 +1（同じ） の範囲に正規化したもの。

内積の定義より，２つのベクトルA,Bがなす角は

つまり，（成分の二乗和の積）分の（成分の積の和）で求められる。

分子は内積で，分母はただの調整用の正の係数だ。

だから，内積とかわらない。違うのは，値の範囲が-1から+1の範囲に正規化されたこと。

この角度が正なら（上げ下げのタイミングの意味で）同傾向，負なら逆傾向である。

（４）共分散：　（２）から，平均のバイアスを取り除いたもの。

離散的な２つの波形A, Bの共分散は

※上付きのバーは平均値を表す。

これは信号A,Bの内積とほとんど変わらない，という点にお気づきだろうか。

内積：

共分散で違うのは，平均からのずれ（＝偏差）つまり「正味の変化」を使って計算している，ということだけだ。

正負の意味も，内積や余弦と同じ。

波形の上がり下がりの傾向を分析する際には，平均なんてものは取っ払ってしまった方がわかりやすい。

だから，共分散は内積がツールとして進化した形であると言える。

計算方法の参考：

共変関係の記述−共分散
http://www.oak.dti.ne.jp/~xkana/psych...

共分散-Wikipedia
http://ja.wikipedia.org/wiki/%E5%85%B...

なお，連続信号どうしの共分散の計算方法は下記で述べた。

2変数関数の相関係数の計算方法と，３次元グラフ描画　（gnuplotで視点をぐりぐり動かす）
http://language-and-engineering.hatenablog.jp/entry/20090126/1232974355

（５）相関係数：　（４）を -1 〜 +1 の範囲に正規化したもの。

（２）の内積が正規化されて（３）の余弦になったように，共分散が正規化されて相関係数となる。

分子は共分散。分母は，いわばどうでもよい調整用の正の係数。

（６）相関関数：　（２）を，あらゆるずらし方について観測したもの。

２つのベクトルをちょっとずらしながら，あらゆるずらし方について内積を取る。

それが相関関数だ。

ただし，存在しない信号値については0埋めする。

内積は「そのまま掛け合わせたら類似するかな？」という試験だった。

こちらでは，「どれぐらいずらしたら類似するかな？」という試験と見ればよい。

相関関数の定義
http://www-lab26.kuee.kyoto-u.ac.jp/s...

まとめ

※上記のグラフをwsf＋Graphvizで描くためのソース

<job>
	<script language="JavaScript" src="DotRecorder.js"></script>
	<script>
	
		var dr = new DotRecorder( "soukan" );
		
		dr.node("kakezan", "かけざん");
		dr.node("naiseki", "内積");
		dr.node("yogen", "なす角の余弦");
		dr.node("kyobunsan", "共分散");
		dr.node("soukankeisu", "相関係数");
		dr.node("soukankansu", "相関関数");
		
		dr.rel("kakezan", "naiseki", "複数点対応");
		dr.rel("naiseki", "yogen", "正規化");
		dr.rel("naiseki","kyobunsan", "バイアス除去");
		dr.rel("kyobunsan","soukankeisu", "正規化");
		dr.rel("naiseki","soukankansu", "ずらしながら");
		
		dr.same_rank( "soukankansu", "naiseki", "kyobunsan" );
		
		dr.dot("soukan.dot");
		dr.png("soukan.png");
		
	</script>
</job>

→http://language-and-engineering.hatenablog.jp/entry/20090123/1232705354